Как связаны радиусы вписанной и описанной окружности - Вписанная, описанная окружность треугольника.
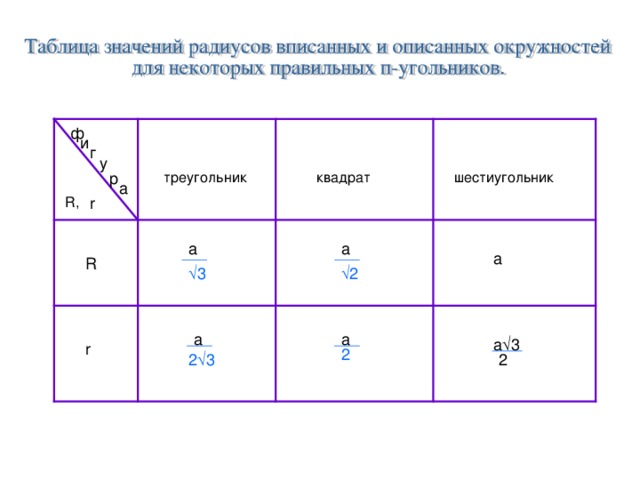
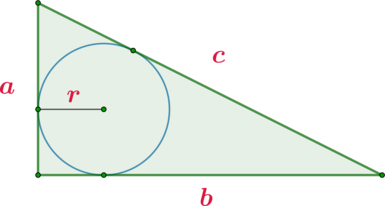
Радиус вписанной окружности в треугольник
Категория: Математика. Похожие презентации:. Описанная окружность. Треугольник, вписанный в окружность.
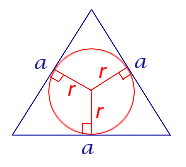
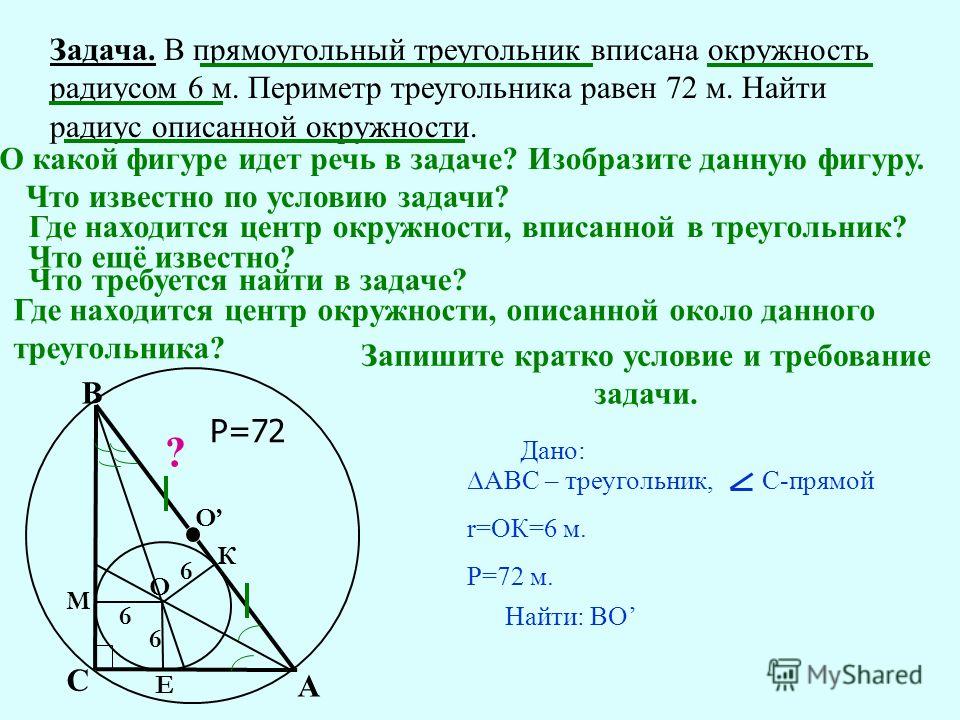



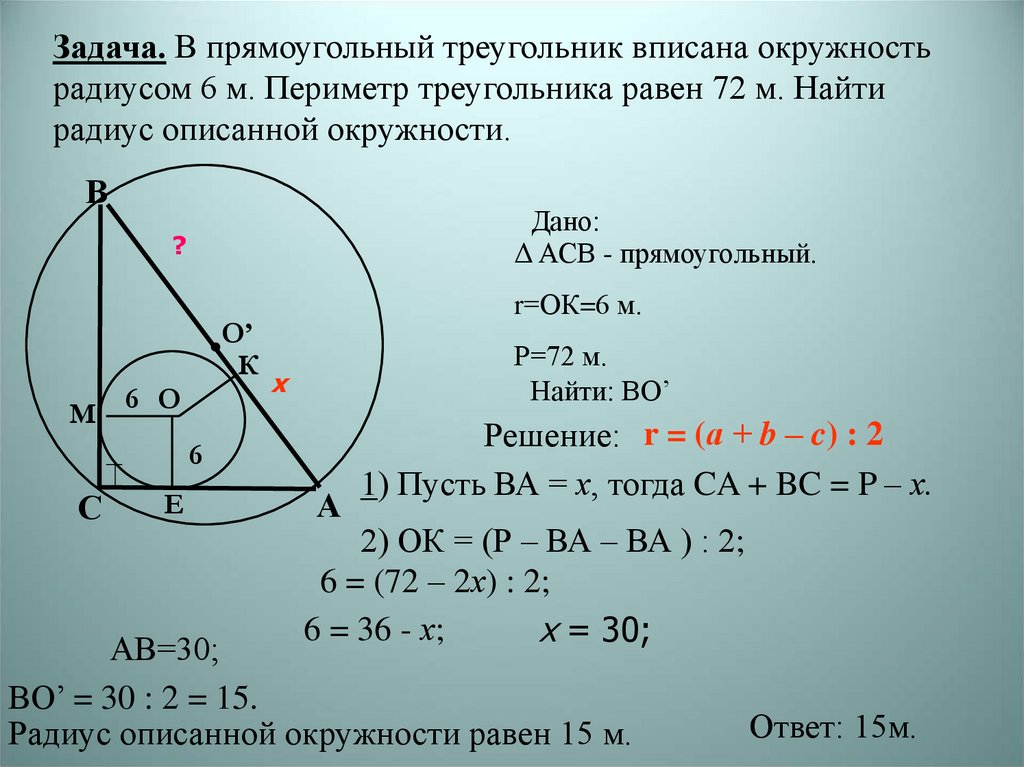
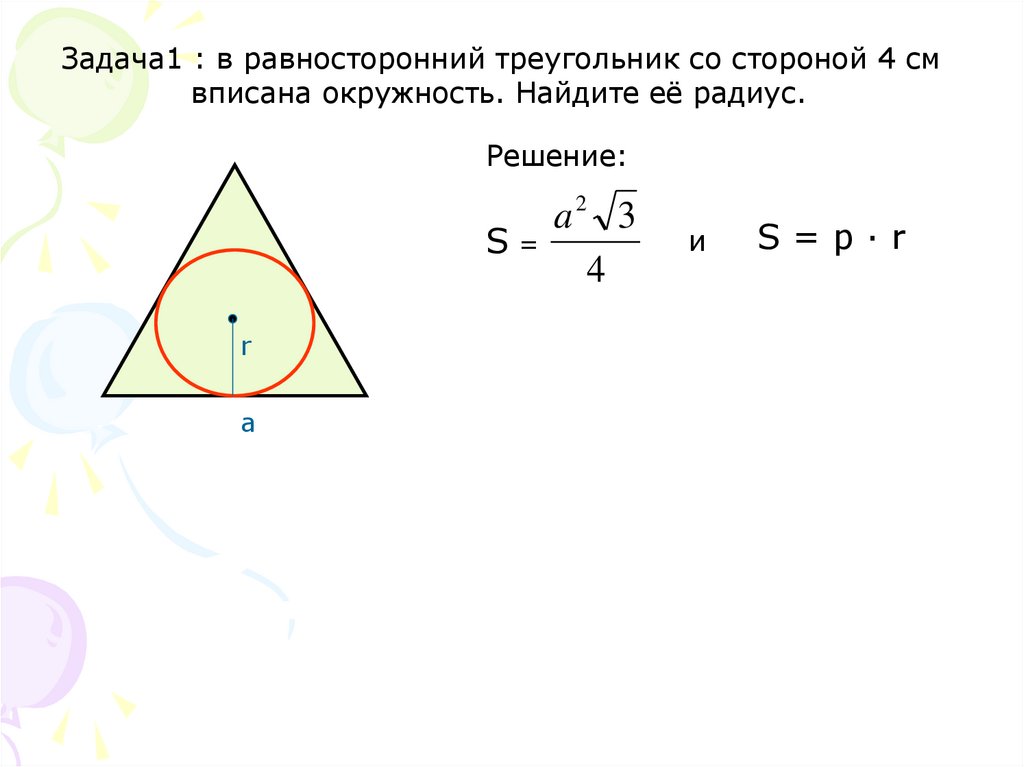
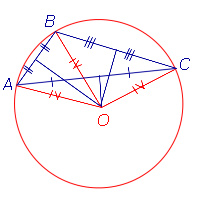

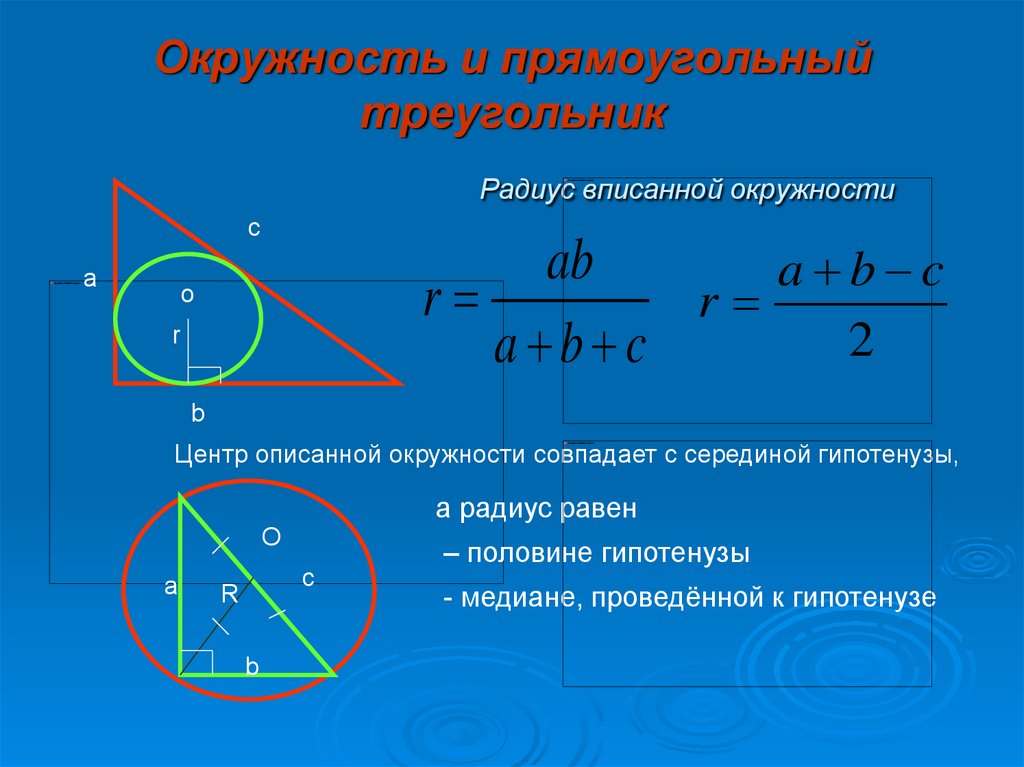


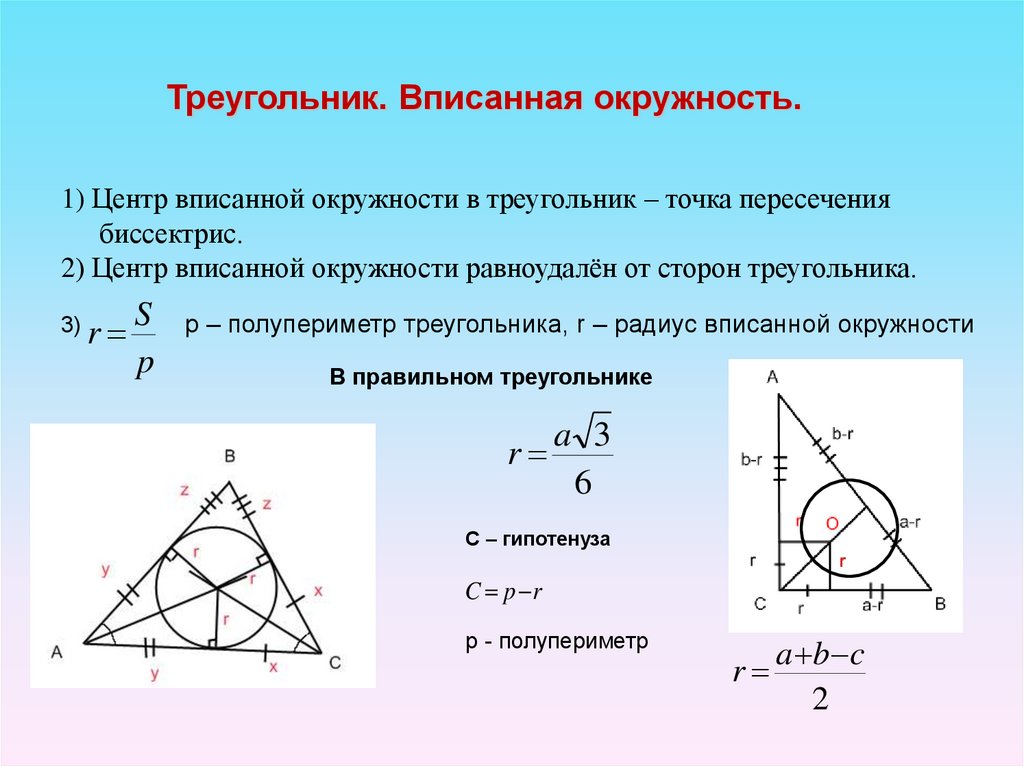
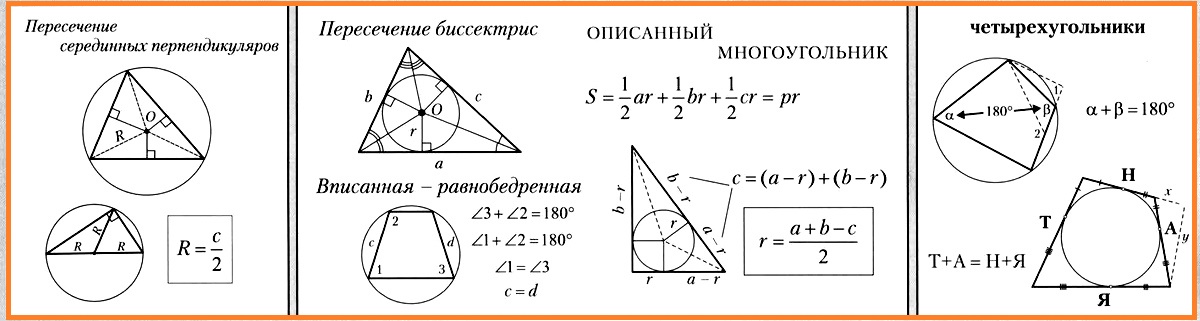
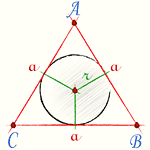
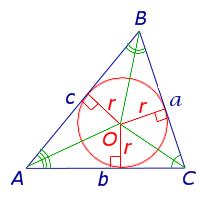
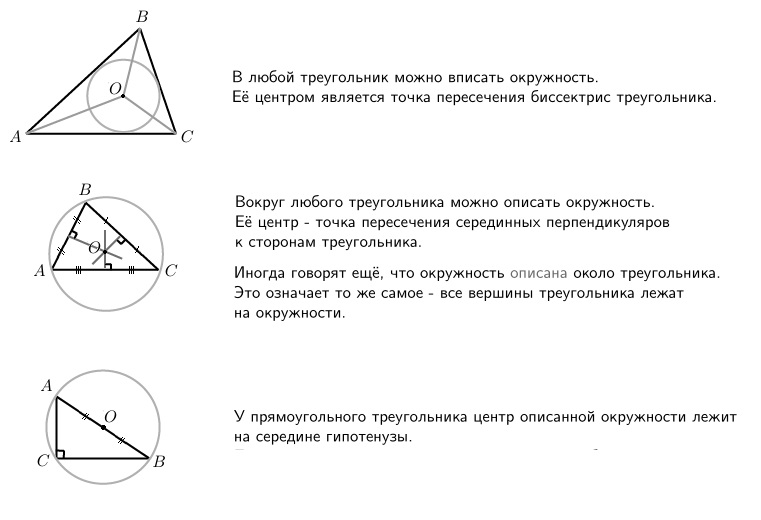
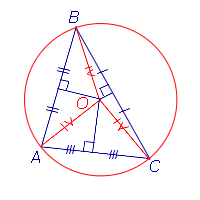
Окружность называется описанной около треугольника, если она проходит через все его вершины. Вместо слов « окружность, описанная около треугольника ABC », также говорят « окружность, описанная вокруг треугольника ABC », или « описанная окружность треугольника ABC ». Теорема об окружности, описанной около треугольника. Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения середенных перпендикуляров в сторонам треугольника. Окружность называется вписанной в треугольник, если она касается всех его сторон.
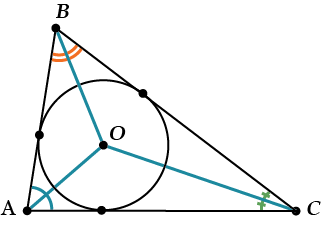






Построение геометрических фигур — одна из основных задач геометрии. Все мы знаем, что для построения треугольника нужно задать его три стороны. Но что, если мы хотим изобразить треугольник, используя только окружности? Кажется, что для изображения треугольника потребуется построить как минимум три окружности — по одной для каждой стороны треугольника.